Here's a really elegant proof for the area of a circle.

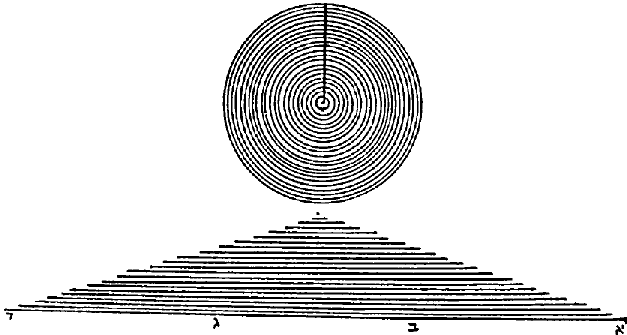
We assume the circle is made up of an infinite number of circular lines. We then straighten the lines out and stack them on top of each other, from longest to shortest. The resulting shape is a triangle. The base of the triangle has length \(2  \pi r \), and the height of the triangle is \(r\), where \(r\) is the radius of the circle.

Then all we need to do is calculate the area of the triangle, which will be:

\[ \frac{base * height}{2} = \frac{(2 \pi r) * r}{2} = \pi r^2 \]